混沌分形之谢尔宾斯基（Sierpinski）-白红宇

混沌分形之谢尔宾斯基（Sierpinski）

阅读量：6039 次

发布时间：2019-06-20

本文共 5272 字，大约阅读时间需要 17 分钟。

本文以使用混沌方法生成若干种谢尔宾斯基相关的分形图形。

（1）谢尔宾斯基三角形

给三角形的3个顶点，和一个当前点，然后以以下的方式进行迭代处理：

a.随机选择三角形的某一个顶点，计算出它与当前点的中点位置；

b.将计算出的中点做为当前点，再重新执行操作a

相关代码如下：

class SierpinskiTriangle : public FractalEquation{public:    SierpinskiTriangle()    {        m_StartX = 0.0f;        m_StartY = 0.0f;        m_StartZ = 0.0f;        m_triangleX[0] = 0.0f;        m_triangleY[0] = FRACTAL_RADIUS;        m_triangleX[1] = FRACTAL_RADIUS*sinf(PI/3);        m_triangleY[1] = -FRACTAL_RADIUS*sinf(PI/6);        m_triangleX[2] = -m_triangleX[1];        m_triangleY[2] = m_triangleY[1];    }    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const    {        int r = rand()%3;        outX = (x + m_triangleX[r])*0.5f;        outY = (y + m_triangleY[r])*0.5f;        outZ = z;    }private:    float m_triangleX[3];    float m_triangleY[3];};

关于基类FractalEquation的定义见：

最终生成的图形为：

通过这一算法可以生成如下图像：

（2）谢尔宾斯基矩形

既然能生成三角形的图形，那么对于矩形会如何呢？尝试下吧：

class SierpinskiRectangle : public FractalEquation{public:    SierpinskiRectangle()    {        m_StartX = 0.0f;        m_StartY = 0.0f;        m_StartZ = 0.0f;        m_ParamA = 1.0f;        m_ParamB = 1.0f;        m_rectX[0] = FRACTAL_RADIUS;        m_rectY[0] = FRACTAL_RADIUS;        m_rectX[1] = FRACTAL_RADIUS;        m_rectY[1] = -FRACTAL_RADIUS;        m_rectX[2] = -FRACTAL_RADIUS;        m_rectY[2] = -FRACTAL_RADIUS;        m_rectX[3] = -FRACTAL_RADIUS;        m_rectY[3] = FRACTAL_RADIUS;    }    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const    {        int r = rand()%4;        outX = (x + m_rectX[r])*0.5f;        outY = (y + m_rectY[r])*0.5f;        outZ = z;    }    bool IsValidParamA() const {
    return true;}    bool IsValidParamB() const {
    return true;}    void SetParamA(float v)    {        m_ParamA = v;        m_rectX[0] = FRACTAL_RADIUS*m_ParamA;        m_rectX[1] = FRACTAL_RADIUS*m_ParamA;        m_rectX[2] = -FRACTAL_RADIUS*m_ParamA;        m_rectX[3] = -FRACTAL_RADIUS*m_ParamA;    }    void SetParamB(float v)    {        m_ParamB = v;        m_rectY[0] = FRACTAL_RADIUS*m_ParamB;        m_rectY[1] = -FRACTAL_RADIUS*m_ParamB;        m_rectY[2] = -FRACTAL_RADIUS*m_ParamB;        m_rectY[3] = FRACTAL_RADIUS*m_ParamB;    }private:    float m_rectX[4];    float m_rectY[4];};

图形如下：

噢，SHIT，毫无规律可言。

那就变动一下吧：

class FractalSquare : public FractalEquation{public:    FractalSquare()    {        m_StartX = 0.0f;        m_StartY = 0.0f;        m_StartZ = 0.0f;        m_rectX[0] = FRACTAL_RADIUS;        m_rectY[0] = FRACTAL_RADIUS;        m_rectX[1] = FRACTAL_RADIUS;        m_rectY[1] = -FRACTAL_RADIUS;        m_rectX[2] = -FRACTAL_RADIUS;        m_rectY[2] = -FRACTAL_RADIUS;        m_rectX[3] = -FRACTAL_RADIUS;        m_rectY[3] = FRACTAL_RADIUS;    }    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const    {        int r = rand()%10;        if (r < 4)        {            outX = (x + m_rectX[r])*0.5f;            outY = (y + m_rectY[r])*0.5f;        }        else        {            outX = x*0.5f;            outY = y*0.5f;        }        outZ = z;    }private:    float m_rectX[4];    float m_rectY[4];};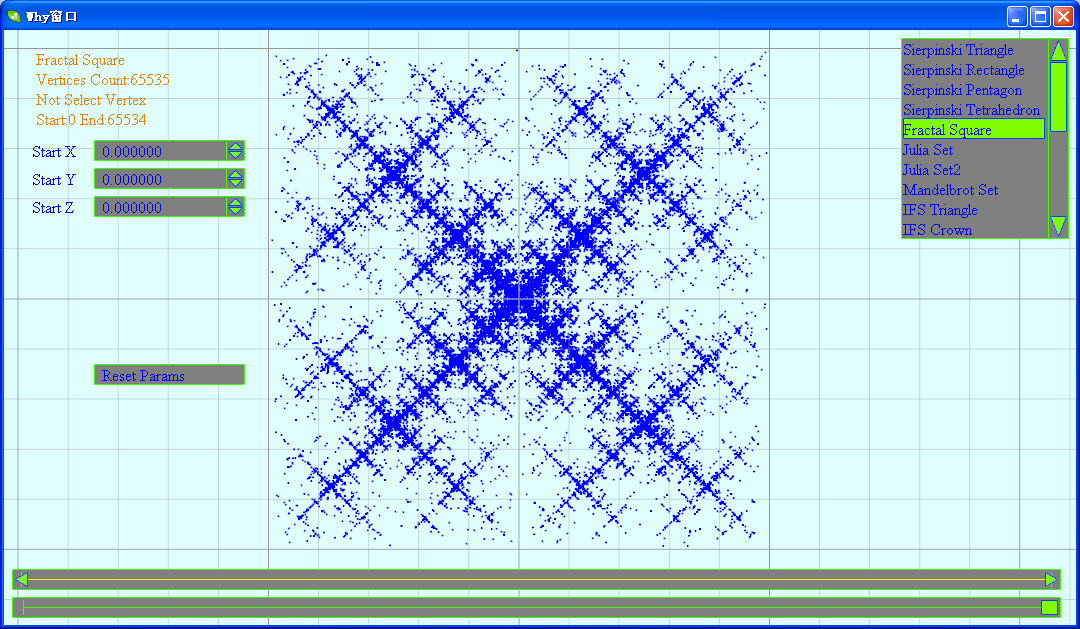

看上去还有点样。

（3）谢尔宾斯基五边形

四边形是不行的，那再试下五边：

// 五边形class SierpinskiPentagon : public FractalEquation{public:    SierpinskiPentagon()    {        m_StartX = 0.0f;        m_StartY = 0.0f;        m_StartZ = 0.0f;        for (int i = 0; i < 5; i++)        {            m_pentagonX[i] = sinf(i*PI*2/5);            m_pentagonY[i] = cosf(i*PI*2/5);        }    }    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const    {        int r = rand()%5;        outX = (x + m_pentagonX[r])*0.5f;        outY = (y + m_pentagonY[r])*0.5f;        outZ = z;    }private:    float m_pentagonX[5];    float m_pentagonY[5];};

有点样子，那就以此算法为基础，生成幅图像看看：

有人称谢尔宾斯基三角形为谢尔宾斯基坟垛，当我看到这幅图时，有一种恐怖的感觉。邪恶的五角形，总感觉里面有数不清的骷髅。

看来二维空间中谢尔宾斯基的单数可以生成分形图形，而双数则为无序的混沌。

（4）谢尔宾斯基四面体

再由二维扩展到三维看看：

class SierpinskiTetrahedron : public FractalEquation{public:    SierpinskiTetrahedron()    {        m_StartX = 0.0f;        m_StartY = 0.0f;        m_StartZ = 0.0f;        m_vTetrahedron[0] = YsVector(0.0f, 0.0f, 0.0f);        m_vTetrahedron[1] = YsVector(0.0f, 1.0f, 0.0f);        m_vTetrahedron[2] = YsVector(YD_REAL_SQRT_3/2, 0.5f, 0.0f);        m_vTetrahedron[3] = YsVector(YD_REAL_SQRT_3/6, 0.5f, YD_REAL_SQRT_3*YD_REAL_SQRT_2/3);        YsVector vCenter = m_vTetrahedron[0] + m_vTetrahedron[1] + m_vTetrahedron[2] + m_vTetrahedron[3];        vCenter *= 0.25f;        m_vTetrahedron[0] -= vCenter;        m_vTetrahedron[1] -= vCenter;        m_vTetrahedron[2] -= vCenter;        m_vTetrahedron[3] -= vCenter;        m_vTetrahedron[0] *= FRACTAL_RADIUS;        m_vTetrahedron[1] *= FRACTAL_RADIUS;        m_vTetrahedron[2] *= FRACTAL_RADIUS;        m_vTetrahedron[3] *= FRACTAL_RADIUS;    }    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const    {        int r = rand()%4;        outX = (x + m_vTetrahedron[r].x)*0.5f;        outY = (y + m_vTetrahedron[r].y)*0.5f;        outZ = (z + m_vTetrahedron[r].z)*0.5f;    }    bool Is3D() const {
    return true;}private:    YsVector m_vTetrahedron[4];};

（5）其他

谢尔宾斯基三角形是一种很神的东西，我写过一些生成图像的算法，常常不知不觉中就出现了谢尔宾斯基三角形。如细胞生长机

再如：

之前我写过几篇与谢尔宾斯基分形相关的文章

转载地址：http://jcrhx.baihongyu.com/

你可能感兴趣的文章